SEGUNDA VALIDACIÓN DEL TEST PSICOMÉTRICO DEL GENIOTIPO

• Nombre del test: Test psicométrico del Geniotipo
• Autor/es del test original: Tony Estruch, Adrià Trujillo y equipo de colaboradores
• Fecha de publicación del test: 2021 – 2022
• Versión del test: 2.3 versión de comercialización
• Fecha de validación: enero 2023 por Juanjo Reyes, investigador graduado en psicología con máster en Psicología del Trabajo y las Organizaciones y máster en Metodología de las Ciencias del Comportamiento y la Salud.
  
  Esta segunda validación del test se realiza para dar continuidad al trabajo llevado a cabo en la construcción del cuestionario.
  Los detalles sobre el instrumento, su proceso de construcción y validación previa están disponibles en una entrada anterior de este blog, a la que se puede acceder a través del siguiente enlace: https://tonyestruch.com/ficha-tecnica-del-cuestionario- del-geniotipo/.
  

1. Método
Todos los análisis realizados para esta segunda validación se llevaron a cabo a través del paquete estadístico R 4.1.2 [1].
En primer lugar, se realizaron análisis descriptivos de las escalas.

En segundo lugar, se realizó un análisis de fiabilidad a partir de los coeficientes Alpha de Crombach y Omega de McDonald con el paquete Pscyh de R [2].

En tercer lugar, se puso a prueba la validez del cuestionario llevando a cabo un Análisis Factorial Confirmatorio (AFC) con el paquete Lavaan de R [3].
Debido a su adecuación para datos de naturaleza ordinal, el estimador utilizado para el cálculo de los parámetros del AFC fue robust unweighted least squares (ULSMV) [4].
El ajuste del modelo se evaluó a través del índice de ajuste absoluto RMSEA (siglas en inglés de Root Mean Square Error of Approximation) y los índices de ajuste relativo CFI (Comparative Fit Index), NNFI (Non-Normed Fit Index), e IFI (Incremental Fit Index) [5].

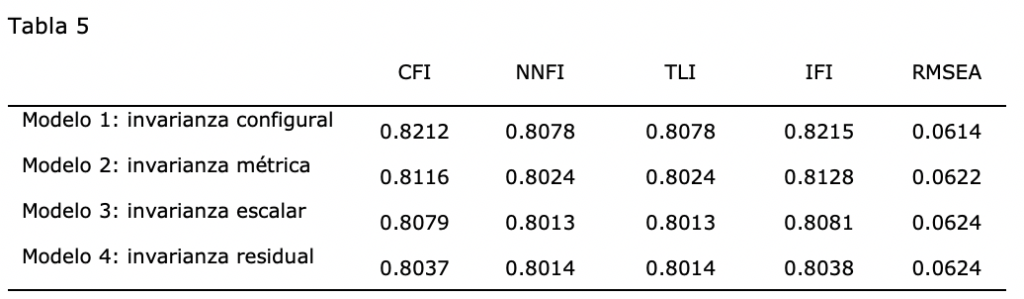
En cuarto lugar, se comprobó si la estructura interna del cuestionario es generalizable a diferentes poblaciones a partir del análisis de invarianza. En particular, se analizaron las diferencias para personas de diferente género (hombres y mujeres) y por región (España y resto de países hispanohablantes).

El análisis de invarianza se llevó a cabo comparando los índices de ajuste de varios modelos construidos con diferentes restricciones en el cálculo de los parámetros, a partir de las cuales se puede establecer si existencia de invarianza configural, métrica, escalar o residual.
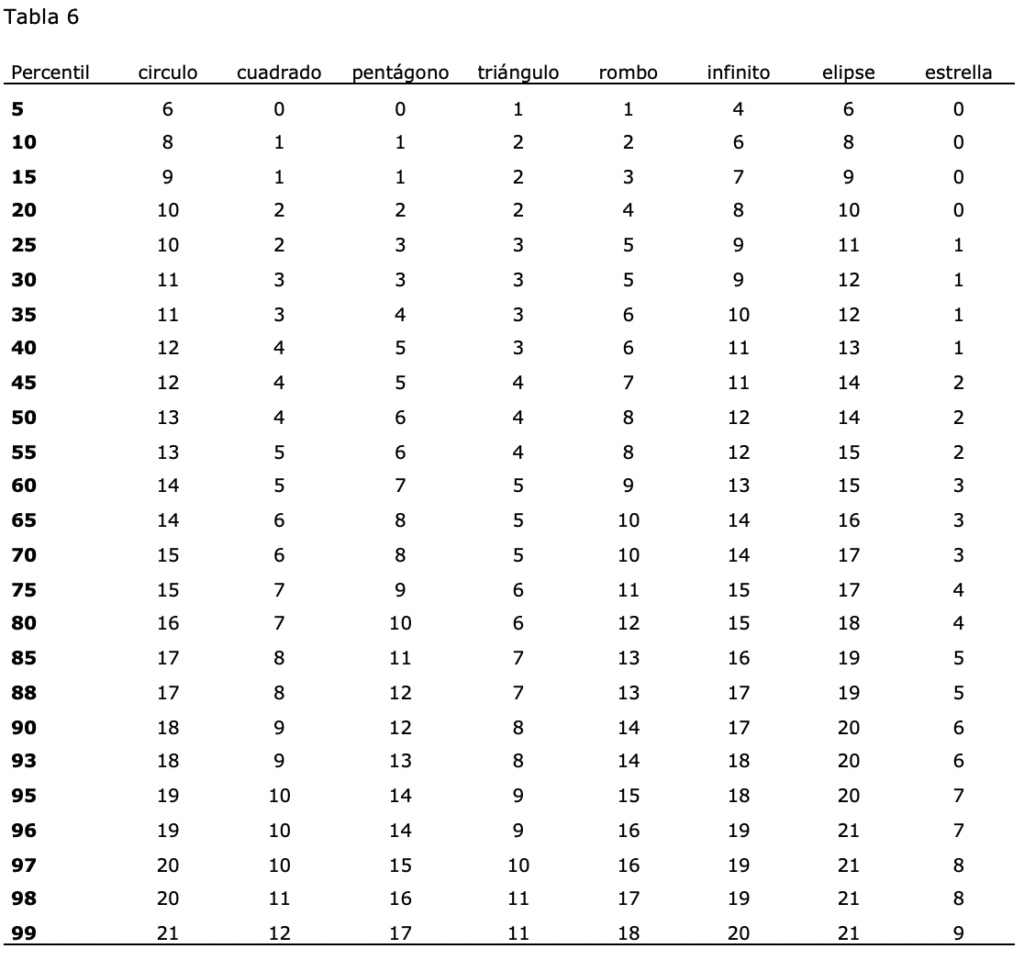
Por último, se realizó una baremación a partir del cálculo de los percentiles.

2. Muestra
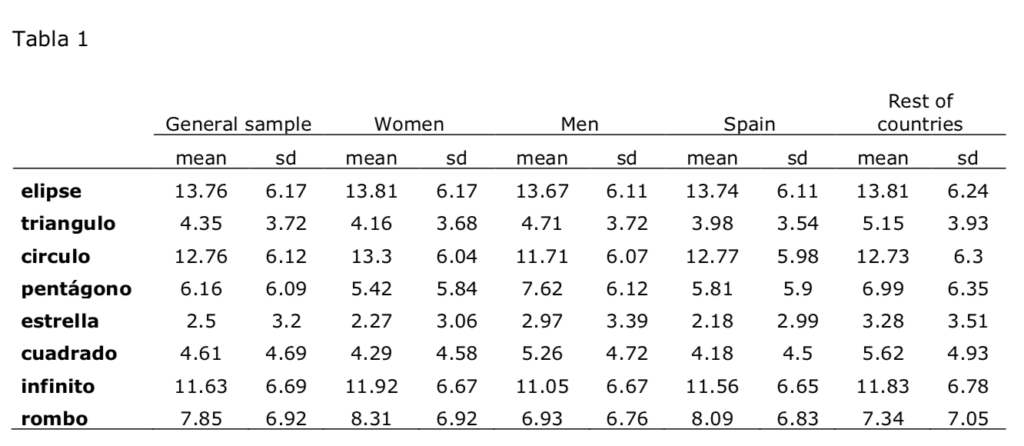
La muestra sobre la que se realizó la validación se compuso de 13.727 personas, de las cuales 9063 (66.03%) eran mujeres y 4664 (33.97%) hombres. Atendiendo a la nacionalidad, 9586 (69.84) personas provenían de España y 4141 (30.16%) de otros países de habla hispana. En la tabla 1 se muestran los valores promedios de las escalas y las desviaciones típicas de cada una de las muestras analizadas.

3. Resultados de las pruebas de fiabilidad
En la tabla 2 se muestran los resultados de las pruebas de fiabilidad. En cuanto al coeficiente alfa de Crombach, existe consenso en considerar valores superiores a .70 adecuados, y valores a partir de .60 aceptables, siendo los valores inferiores a .50 inaceptables [6]. Estos mismos criterios cuantitativos son aplicables al coeficiente Omega de McDonald.

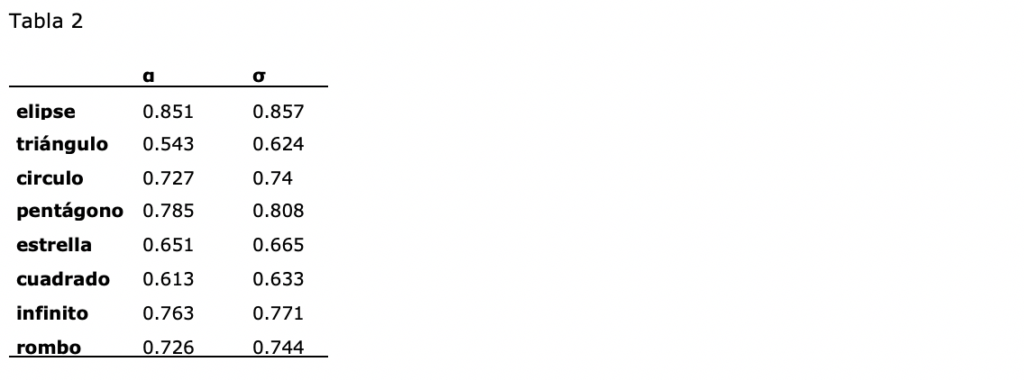
4.Resultados del Análisis Factorial Confirmatorio
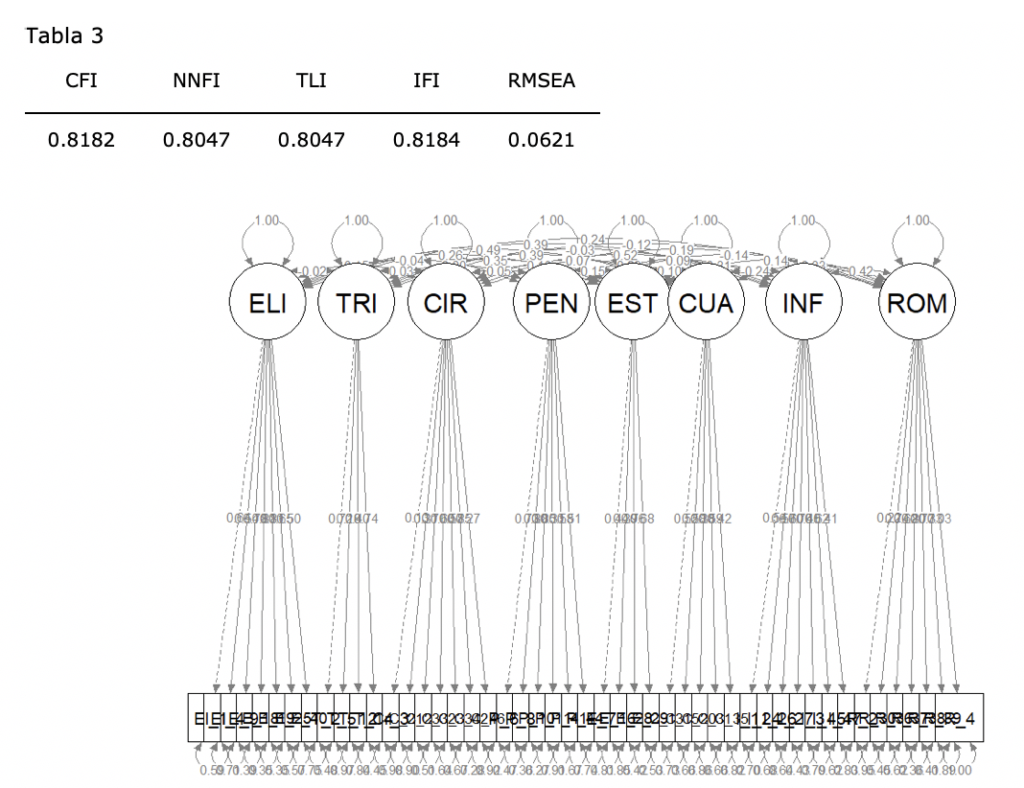
En la tabla 3 se muestran los índices de ajuste relativos y absolutos del AFC. Para los índices de ajuste absolutos (CFI, NNFI, TLI, IFI) se considera que existe un buen ajuste del modelo cuando los índices cuentan con valores superiores a .90 [7]. Para el índice de ajuste absoluto RMSEA, valores inferiores a .05 se consideran excelentes, mientras que valores inferiores a .08 se consideran aceptables [8].

El análisis de las cargas factoriales de los diferentes ítems muestran que en las escalas triángulo, círculo, pentágono, cuadrado y rombo existen ítems con valores estandarizados inferiores a .4, el cual es considerado criterio de corte para evaluar la relevancia de un ítem en el factor [9].

5.Resultados del análisis de invarianza
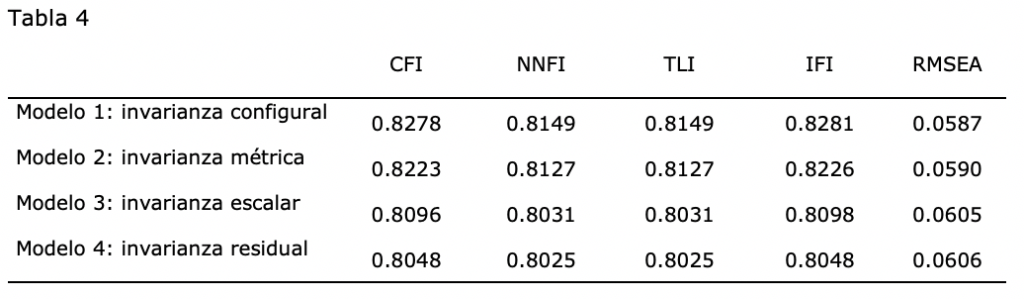
El criterio seguido para la valorar magnitud del cambio de ajuste entre modelos se estimó a partir de las diferencias en los índices de ajuste absoluto y relativos propuestos. Incrementos bajos en esos índices (Δ<.01) indican invariancia entre modelos [10].

5.1 Invarianza por género
El incremento en los índices de ajuste entre los modelos es menor a .01 en todos los casos, lo que indica que la estructura interna propuesta es invariante. La diferencia entre los índices del modelo con mejor ajuste, el modelo sin restricciones (Modelo 1), y el modelo con restricción en las cargas factoriales y las intersecciones de los ítems (Modelo 3) es superior al criterio establecido de .01, por tanto, se considera que el modelo cuenta con invarianza métrica (restricción en las cargas factoriales, Modelo 2).

5.2 Invarianza por región
Las diferencias entre los modelos son inferiores a .01, por lo que existe un alto grado de invarianza. El modelo sin restricciones (Modelo 1) es el que mejor ajuste muestra. La diferencia entre los índices de este modelo frente a los del modelo de invarianza escalar (Modelo 3) son superiores a .01, por lo que se puede concluir con que el modelo cuenta con invarianza métrica entre regiones.

6. Baremos
Percentil circulo cuadrado pentágono triángulo rombo infinito elipse

7. Conclusiones
Los resultados de la validación muestran que las escalas tienen una fiabilidad de aceptable (cuadrado, estrella) a excelente (elipse, círculo, pentágono, infinito, rombo), a excepción de la escala utilizada para evaluar la dimensión triángulo, para la que se recomienda realizar una revisión de los ítems incluidos.

Los resultados del AFC muestran que la estructura interna de la escala es aceptable. El índice de ajuste absoluto RMSEA se enmarca entre los valores aceptables (.05 y .08). Los índices de ajuste relativo (CFI, NNFI, TLI e IFI) se desvían sensiblemente del valor consensuado por la comunidad científica de .90. En cinco de las escalas (triángulo, círculo, pentágono, cuadrado y rombo) varios ítems muestran cargas factoriales inferiores a .4, lo cual es indicativo de que no están aportando información relevante para el cálculo de la puntuación del factor.

La estructura interna de la escala es invariante entre muestras a nivel métrico, lo que indica que el peso factorial de cada ítem en la escala a la que pertenece es similar entre géneros y regiones.

7.1 Conclusión resultante
A partir de los resultados obtenidos en la segunda validación, se concluye que el cuestionario cuenta con niveles de fiabilidad y validez aceptables para su uso profesional, según el estándar consensuado por la comunidad científica. La prueba muestra margen de mejora, especialmente en los ítems de evaluación del tipo Triángulo. En cualquier caso, dichos estándares fueron alcanzados en la primera validación realizada del test, realizada sobre una muestra independiente. La estructura interna de la prueba se muestra sólida y transversal en muestras de diferente género y región geográfica, lo cual garantiza la generalización de resultados en poblaciones diversas en cuanto a dichas características. La prueba ha sido validada siguiendo un proceso riguroso, poco habitual en contextos no académicos.

Como próximos pasos, se propone realizar análisis pormenorizados de los ítems que componen las diferentes escalas para mejorar el ajuste de las mismas y explorar nuevos procedimientos de validación.

8. Certificación de resultados
La validación de la prueba ha sido desarrollada de manera independiente por Juanjo Reyes, investigador graduado en psicología con máster en Psicología del Trabajo y las Organizaciones y máster en Metodología de las Ciencias del Comportamiento y la Salud, quien declara no tener conflictos de interés a la hora de realizar la validación.

9. Referencias
[1] R Core Team (2021). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.

[2] Revelle, W. (2017) psych: Procedures for Personality and Psychological Research, Northwestern University, Evanston, Illinois, USA, https://CRAN.R-project.org/package=psych Version = 1.7.8.

[3] Rosseel Y (2012). “lavaan: An R Package for Structural Equation Modeling.” Journal of Statistical Software, 48(2), 1–36. https://www.jstatsoft.org/v48/i02/.

[4] Kilic, A. F., & Dogan, N. (2021). Comparison of confirmatory factor analysis estimation methods on mixed-format data. International Journal of Assessment Tools in Education, 8(1), 21-37.

[5] Bentler, P. M. (1990). Comparative fit indexes in structural models. Psychological bulletin, 107(2), 238.

[6] Frías-Navarro, D. (2022). Apuntes de estimación de la fiabilidad de consistencia interna de los ítems de un instrumento de medida. Universidad de Valencia. España. Disponible en: https://www.uv.es/friasnav/AlfaCronbach.pdf

[7] Hu, L. T., & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural equation modeling: a multidisciplinary journal, 6(1), 1-55.

[8] Browne, M. W., & Cudeck, R. (1993). Alternative ways of assessing model fit. In K. A. Bollen & J. S. Long (Eds.), Testing structural equation models (pp. 136-62), Newbury Park, CA: Sage

[9] Guadagnoli, E., & Velicer, W. F. (1988). Relation of sample size to the stability of component patterns. Psychological bulletin, 103(2), 265.

[10] Cheung, G. W., & Rensvold, R. B. (2002). Evaluating goodness-of-fit indexes for testing measurement invariance. Structural equation modeling, 9(2), 233-255.